Wally Saves Tammy from the Well
Oh no! Tammy (20 kg) has fallen into the well at the top of the hill. Wally (45 kg) stands near the top of the frictionless slope, which is at a 35° incline to the horizontal. A rope runs over a frictionless pulley to the bottom of the well.
Question 1: If Wally and Tammy hold onto opposite ends of the rope, what is the net force acting on them?
There are three forces acting on Wally: a gravitational force, a normal force from the slope, and a force of tension from the rope.
There are two forces acting on Tammy: a gravitational force and a force of tension from the rope.
We will sketch our problem and orient our coordinate system so that the positive x-axis is in line with the direction of motion.
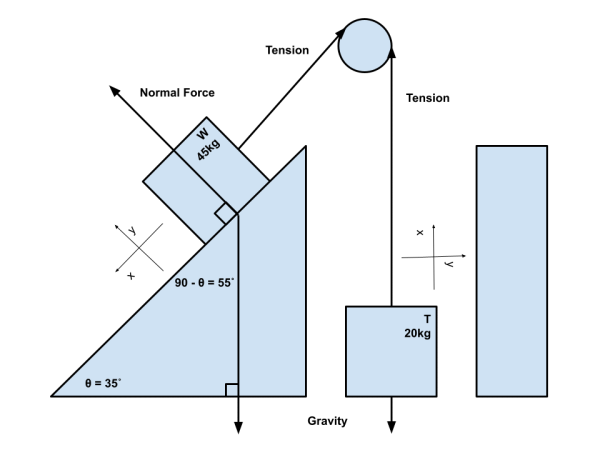
Figure 1: Our Sketch of the Forces Acting on Wally & Tammy
Note that our direction of motion bends around the pulley, so our coordinate system follows accordingly.
Let's look at the forces one by one. For the gravitational force on Wally, we're only concerned with it's x-component, as that is what it contributes in the direction of motion. We can utilize trigonometric ratios to derive this:
\[ F_{\text{w.gravity}_\text{x}} = F_{\text{w.gravity}} \times \cos( 90^\circ - \theta) \]
\[ F_{\text{w.gravity}_\text{x}} = m_\text{w} \times g \times \cos( 90^\circ - \theta) \]
The gravitational force on Tammy is in line with the direction of motion, so it contributes its full magnitude. Note, however, that it's directed opposite the direction to the motion, so its value is negative:
\[ F_{\text{t.gravity}_\text{x}} = F_{\text{t.gravity}} \]
\[ F_{\text{t.gravity}_\text{x}} = - \, m_\text{t} \times g \]
The normal force on Wally is perpendicular to the direction of motion. Therefore, it does not contribute:
\[ F_{\text{w.normal}_\text{x}} = 0 \]
Finally, we know the sum of tensional forces on Wally and Tammy is zero, because they are of equal magnitude in opposite directions.
\[ F_{\text{w.tension}_\text{x}} + F_{\text{t.tension}_\text{x}} = 0 \]
Therefore, we can calculate the value for the net force:
\[ F_\text{net} = F_{\text{w.gravity}_\text{x}} + F_{\text{t.gravity}_\text{x}} + F_{\text{w.normal}_\text{x}} + ( F_{\text{w.tension}_\text{x}} + F_{\text{t.tension}_\text{x}} ) \]
\[ F_\text{net} = (m_\text{w} \times g \times \cos( 90^\circ - \theta)) - (m_\text{t} \times g) + (0) + (0) \]
\[ F_\text{net} = (m_\text{w} \times \cos( 90^\circ - \theta) - m_\text{t} ) \times g \]
\[ F_\text{net} = (45 \, \text{kg} \times \cos( 90^\circ - 35^\circ) - 20 \, \text{kg} ) \times 9.8 \, \text{m/s}^2 \]
\[ F_\text{net} \approx 56.95 \, \text{N} \]
Question 2: What is the magnitude of their acceleration?
We can apply Newton's Second Law of Motion to calculate the acceleration of the system. Note we use the combined weight of Wally and Tammy, since they're both moving.
\[ F_\text{net} = (m_\text{w} + m_\text{t}) \times a \]
Rearranging the equation to solve for \(a\) and plugging in known values, we arrive at our answer:
\[ a = F_\text{net} / (m_\text{w} + m_\text{t}) \]
\[ a \approx (56.95 \, \text{N}) / ((45 \, \text{kg}) +(20 \, \text{kg})) \]
\[a \approx 0.88 \, \text{m/s}^2 \]
Question 3: What is the tension in the rope?
Again, we use Newton's Second Law of Motion, but this time, just with respect to Tammy's situation. We have everything we need now from our previous calculations to solve:
\[ F_{\text{t.tension}_\text{x}} + F_{\text{t.gravity}_\text{x}} = m_\text{t} \times a \]
Rearranging, and solving for \(F_{\text{t.tension}_\text{x}}\), we arrive at our answer:
\[ F_{\text{t.tension}_\text{x}} = m_\text{t} \times a - F_{\text{t.gravity}_\text{x}} \]
\[ F_{\text{t.tension}_\text{x}} = m_\text{t} \times a - (- m_\text{t} \times g) \]
\[ F_{\text{t.tension}_\text{x}} \approx (20 \, \text{kg}) \times (0.88 \, \text{m/s}^2) - (- (20 \, \text{kg}) \times (9.8 \, \text{m/s}^2)) \]
\[ F_{\text{t.tension}_\text{x}} \approx 213.60 \, \text{N} \]