Wally Drives Down a Windy Road
Wally is a speed demon. He drives his 1000 kg car down a windy road. He rounds a circular bend of radius 60 m at a speed of 20 m/s.
Question 1: What is the centripetal acceleration of Wally's car?
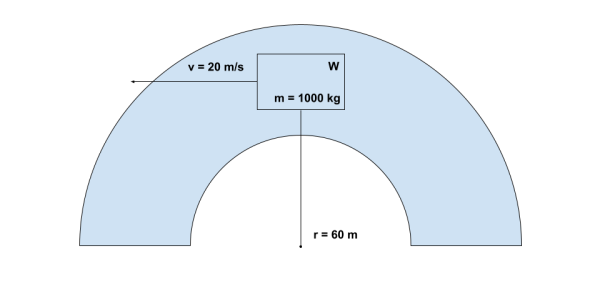
Figure 1: Our Sketch of the Problem
The formula for centripetal acceleration of an object is its speed squared, divided by the radius:
\[ a_\text{cp} = v^2/r \]
Substituting the given values for speed and radius, we can calculate its value:
\[ a_\text{cp} = ( 20 \, \text{m/s} )^2 / (60 \, \text{m}) \]
\[ a_\text{cp} \approx 6.7 \, \text{m/s}^2 \]
Question 2: What is the centripetal force required to keep Wally on the road?
Using Newton's Second Law for circular motion, we know that the centripetal force on an object is equal to its mass times the centripetal acceleration:
\[ F_\text{cp} = m \times a_\text{cp} \]
Substituting the mass of the car from our given information and our calculated \( a_\text{cp} \), we can calculate the value:
\[ F_\text{cp} \approx ( 1000 \, \text{kg} ) \times 6.7 \, \text{m/s}^2 \]
\[ F_\text{cp} \approx 6700 \, \text{N} \]